Understanding the Significance of 90-7.814 in Precision

Precision is critical because even small deviations in calculations can lead to large errors, especially in fields like engineering, economics, and science. Accurate calculations ensure the success and reliability of projects, models, and predictions.
The expression itself equates to 82.186, but this seemingly simple calculation has far-reaching implications in fields ranging from engineering to economics.

In many technical and scientific fields, precision in calculations is paramount, and even small differences can lead to significantly different outcomes. Thus, this basic operation is often used as a stepping stone to illustrate the importance of accuracy in more complex scenarios. Whether it’s adjusting measurements in construction or fine-tuning financial models, understanding the importance of 90-7.814 can help to build stronger systems and models that rely on exact values.

The Importance of Precision in Calculations

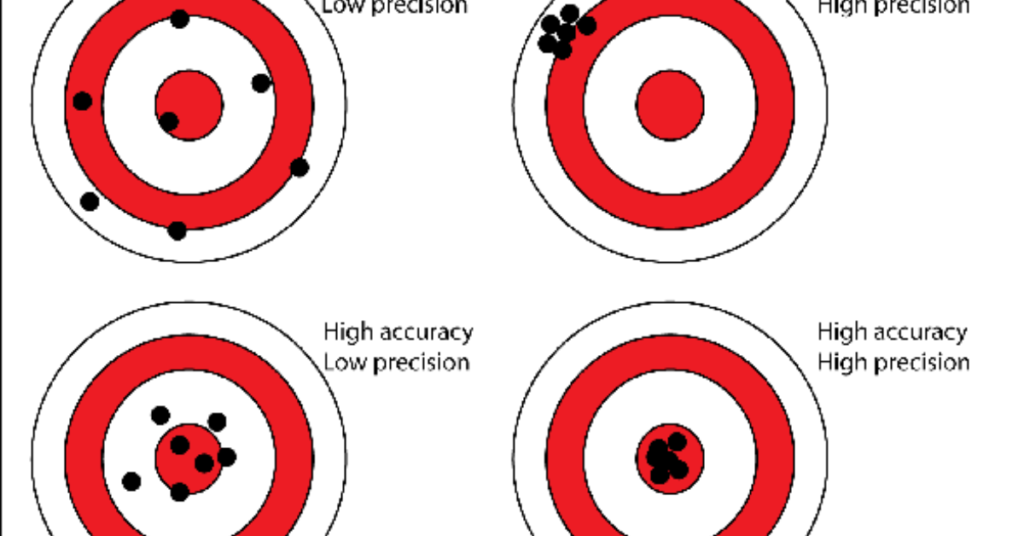
In industries like engineering, physics, and economics, the value of precision cannot be overstated. A slight deviation of a few decimal places can affect the results of experiments, design measurements, or financial projections. In many instances, calculations like “90-7.814” are the first step in larger models that rely on exact values. Therefore, mastering precision is essential to minimizing errors and ensuring that systems and models work as expected.

When working in fields that require precise measurements—whether you’re designing a structural 

engineering project, conducting a scientific experiment, or analyzing the latest market trends—small errors in calculations can snowball, leading to catastrophic consequences. From a financial model misjudging the price of goods to engineering calculations causing a design to fail, even a minor mistake can have serious repercussions.

Why “90-7.814” Matters in Multiple Disciplines

The expression “90-7.814” is not just confined to the classroom or textbooks; it finds real-world applications in diverse fields. In structural engineering, this subtraction might be part of a series of measurements required to ensure that two pieces of material fit together perfectly. In economic forecasting, “90-7.814” could represent a financial adjustment in a larger model. For scientific calculations, it might be part of an experimental design where precise adjustments are necessary to validate a hypothesis. The significance of this simple calculation extends beyond arithmetic and underscores the vital role that precision plays in shaping the world around us.

Mathematical Interpretation of 90-7.814

The Basic Arithmetic Operation

At its most basic level, “90-7.814” is a straightforward arithmetic operation where 7.814 is subtracted from 90, resulting in 82.186. However, this simple subtraction serves as a model for how more complex equations and formulas work. It is a foundational step in mathematical precision, where decimal places matter just as much as whole numbers.

In this context, it is important to recognize that decimals represent fractions of a whole, making them crucial in real-world calculations where the smallest deviations can have significant consequences. Whether it’s calculating an angle, adjusting measurements, or determining a financial factor, the difference between 90 and 7.814 plays a key role in achieving accurate results.

Significance of Decimal Places in Mathematical Precision

Decimals are not just numbers after a point; they represent an entirely different level of precision. For example, 7.814 in “90-7.814” conveys specific, granular information that cannot be captured by rounding to the nearest whole number. Such decimal precision is important in areas like engineering calculations, where structural components must be designed to exact dimensions. In scientific calculations, slight decimal adjustments can affect experimental results and lead to different interpretations of data.

Every decimal place in a calculation like 90-7.814 has meaning, and understanding that significance is crucial in any field that requires precision. This is especially true when performing mathematical operations in fields like physics, engineering, and economics, where even the smallest margin of error can lead to faulty predictions or unsafe designs.

Why Every Digit Matters in Engineering and Science

In engineering and science, precision is not just a luxury; it is a necessity. A slight error, such as a miscalculation involving the subtraction of 7.814 from 90, can affect the integrity of a product or the validity of an experiment. For example, in structural engineering calculations, even minor discrepancies can lead to building flaws or safety hazards. In scientific research, precise data is crucial for achieving accurate and reproducible results. Without precision, conclusions drawn from experiments would be unreliable, making “90-7.814” a small but important example of how every digit can have an impact.

Real-World Applications in Science and Engineering

Structural Engineering: Ensuring Accurate Measurements

In structural engineering, every design must be based on precise measurements to ensure safety and functionality. The subtraction operation 90-7.814 might represent the adjustment of a structural component’s size to fit into a designated space. A structural beam that is 90 units long might need to be adjusted by 7.814 units to align with other components, ensuring a secure fit. These kinds of calculations are essential when working with large-scale projects such as bridges, buildings, or roadways, where even small adjustments can make a big difference.

By understanding the importance of these precise calculations, engineers can design better structures, optimize materials, and prevent errors that could lead to costly mistakes. Whether calculating dimensions for CAD software or fine-tuning measurements on a construction site, engineering relies heavily on accurate calculations like 90-7.814.

Fine-Tuning Measurements in Physics Experiments

In physics, the precision of measurements is critical to obtaining meaningful results. Experiments often involve adjusting variables by small amounts, like subtracting 7.814 from 90, to account for things like error margins or measurement uncertainties. Whether calculating the trajectory of a particle, adjusting the settings of a particle accelerator, or conducting other high-precision experiments, every digit can impact the accuracy of the outcome.

In this way, 90-7.814 serves as an example of how even basic calculations are crucial in more complex scientific experiments. The precision of the result might influence further calculations or determine the success of the experiment, making every decimal place significant.

Electronics and Circuit Design Adjustments

In the field of electronics, precision in measurements is required to design and tune electrical components such as resistors, capacitors, and circuit boards. When designing a circuit, engineers may need to make small adjustments, similar to subtracting 7.814 from 90, to ensure the correct flow of current and prevent malfunction. These adjustments can make the difference between a properly functioning device and one that doesn’t work as intended.

Whether it’s optimizing electrical components or designing a microchip, the need for precision in calculations like 90-7.814 is fundamental to ensuring the reliability of technological innovations.

Case Study: Engineering Precision with 90-7.814

Consider an example in structural design, where a beam is meant to fit into a space measuring 90 units long. After a precise measurement, it is found that the beam needs to be shortened by 7.814 units to align perfectly with the surrounding components. By accurately subtracting 7.814, the engineer ensures the beam fits perfectly and the structure remains safe and functional. This is a small but essential task in the broader context of engineering design that highlights the significance of mathematical precision.

Economic Implications of 90-7.814

Cost Analysis in Financial Models

In economic forecasting and financial analysis, precise calculations are required to predict costs and returns accurately. “90-7.814” might represent an adjustment in the value of a product or asset. For example, 7.814 could represent a cost factor that needs to be subtracted from a baseline value of 90 to determine the final price of a good or service.

Accurate cost analysis ensures that companies can make informed decisions about cost optimization and pricing strategies, preventing loss and maximizing profitability. Financial models often rely on such precise calculations to forecast future trends and make data-driven decisions.

Statistical Adjustments for Economic Forecasting

Economic forecasting involves predicting future trends based on current data. Precision is key in ensuring that predictions are as accurate as possible. By using calculations like 90-7.814, economists can adjust data to account for various factors such as inflation, market shifts, or unforeseen events. These adjustments ensure that the forecast reflects the most up-to-date and reliable information available.

Through statistical modeling, economists can use precise data adjustments to predict everything from stock market trends to unemployment rates, ensuring that their models are as accurate as possible.

Depreciation and Asset Value Adjustments

In economics, “90-7.814” could also be used to adjust the value of assets over time. Depreciation is a concept used to account for the reduction in value of an asset over its lifespan. For example, a vehicle or property might be initially valued at 90 units, but after accounting for depreciation, a small adjustment like 7.814 might be necessary. This adjustment helps businesses accurately reflect the true value of their assets in financial reports, which is crucial for making informed investment decisions.

Real-Life Example: Economic Forecasting with Precision

In the realm of economic forecasting, precise adjustments are crucial to ensuring that predictions reflect reality as accurately as possible. For instance, when estimating the future costs of an infrastructure project, small differences like the result from 90-7.814 can significantly affect the final budget estimates. In a situation where a project’s baseline cost is 90 units, subtracting 7.814 units for unforeseen expenses like material shortages or labor costs can fine-tune the economic projection, making it more reliable for financial decision-making.

Financial analysts often rely on precise calculations like this to model cost optimizations, evaluate asset values, or project future expenditures, which all play critical roles in keeping organizations solvent and competitive.

Precision in Scientific Calculations

Error Margin Adjustments in Research

In research, especially in scientific fields, adjusting for error margins is an essential part of the process. Error margins refer to the small deviations that can arise due to limitations in measuring instruments, human errors, or the variability of materials. By carefully adjusting measurements, such as through a subtraction like 90-7.814, researchers can account for these inconsistencies and achieve more accurate results.

For example, when conducting a scientific experiment, precise measurements are vital for obtaining reproducible results. Even the smallest inaccuracies can lead to unreliable conclusions, which is why scientists take extra care in ensuring that all calculations, including those as simple as 90-7.814, are carried out with the highest precision possible.

Unit Conversions and Their Impact

In the world of scientific calculations, unit conversions play a pivotal role. The process of converting between different units—whether from meters to kilometers or from grams to kilograms—requires precise mathematical operations. “90-7.814” might be used in such conversions, where minor adjustments ensure that the final outcome is consistent with the required units. Small errors in these conversions can lead to significant discrepancies, especially in fields like physics and chemistry, where even a slight change in measurements can influence experimental outcomes.

By understanding and implementing exact mathematical steps, such as subtracting 7.814 from 90, scientists can maintain the integrity of their data and ensure that the final results are consistent with their hypotheses.

 Enhancing Accuracy in Research through Small Adjustments

Even the smallest of calculations, like 90-7.814, can play a crucial role in improving the accuracy of scientific research. In the process of data collection and analysis, making small adjustments based on precise calculations ensures that the overall findings are as accurate as possible. Whether it’s adjusting the weight of a sample in a lab or calibrating instruments in a high-tech research environment, mathematical precision is integral to obtaining reliable results. Researchers use these adjustments to avoid measurement errors, ultimately contributing to the advancement of scientific knowledge.

Challenges in Using 90-7.814

Addressing Rounding Errors

One of the key challenges in working with numbers like 90-7.814 is avoiding rounding errors. Rounding errors occur when a calculation is approximated to fewer decimal places, leading to a potential loss in precision. For instance, rounding the result of 90-7.814 to 82.19 instead of 82.186 could introduce a small discrepancy, which might not seem significant at first but could compound in larger calculations.

In both engineering and financial modeling, addressing rounding errors is crucial for ensuring the integrity of results. Small rounding errors can lead to significant discrepancies, particularly when these calculations are used to guide important decisions, such as determining the cost of a construction project or predicting the behavior of financial markets.

Misinterpretation of Simple Calculations

Another challenge with calculations like 90-7.814 is the risk of misinterpretation. While the equation itself is straightforward, its context and the level of precision required may be overlooked. In engineering or financial forecasting, misinterpreting or over-simplifying such calculations can lead to incorrect conclusions.

For instance, engineers may need to make a series of calculations based on measurements that require consistent adjustments. Misinterpreting the decimal places in such basic operations can affect the final results, potentially compromising safety and functionality. Therefore, it’s essential to consider every detail when interpreting simple calculations like 90-7.814.

The Risk of Overlooking Minor Adjustments in Complex Models

In fields like economic forecasting or structural engineering, overlooking small adjustments in seemingly minor calculations can have significant consequences. A calculation like 90-7.814, though simple, could form part of a larger model that influences major decisions. If an adjustment is missed or not properly accounted for, it could lead to cost overruns, inaccurate financial projections, or flawed engineering designs.

In many real-world applications, the cumulative effect of multiple small miscalculations can lead to large-scale issues, which is why precision and attention to detail are so important. Ensuring that minor calculations like 90-7.814 are correct is a critical step in building reliable models and systems.

Technological Tools for Precision

Digital Calculators and Software Solutions

To achieve the level of precision required in fields like engineering and economics, professionals often rely on advanced tools such as digital calculators and specialized software. These tools ensure that every calculation, whether it’s 90-7.814 or a more complex operation, is executed with the highest level of accuracy possible.

Engineering software like AutoCAD or Revit helps architects and designers model structures down to the smallest measurements, ensuring that every component fits together perfectly. Similarly, financial modeling software uses complex algorithms to incorporate precise adjustments, ensuring that projections and cost analyses are as accurate as possible.

The Role of CAD Software in Engineering Design

In structural design, CAD software plays a vital role in ensuring that every measurement and calculation is precise. The use of CAD allows engineers to model a building or infrastructure project with exacting measurements, like subtracting 7.814 from 90 to make adjustments. These software solutions enable designers to see how their decisions impact the overall project, helping to minimize errors before physical construction begins.

By integrating precision into the design process, CAD software ensures that every measurement and calculation is accurate, ultimately contributing to the safety and success of the project.

Advanced Tools in Financial Modeling and Data Science

In the world of data science and financial modeling, advanced tools like statistical software and machine learning algorithms are used to refine calculations and forecasts. These tools are designed to handle complex models that rely on precise inputs, such as 90-7.814, to ensure that every prediction is as accurate as possible. Whether it’s predicting market trends, optimizing financial portfolios, or adjusting for inflation, these tools rely on mathematical precision to deliver reliable results.

Future Perspectives on Precision in Calculations

The Growing Need for Accurate Data in AI and Machine Learning

As artificial intelligence (AI) and machine learning continue to advance, the demand for accurate data and calculations is expected to grow exponentially. AI systems rely on precise data to make predictions, and even the smallest deviations in input data, like 90-7.814, can lead to vastly different outcomes. The need for precision in AI-driven systems will become increasingly important, particularly in industries like healthcare, autonomous vehicles, and financial trading, where small errors can have significant real-world consequences.

Automation of Precise Calculations in Future Technologies

The future of automated calculations in fields like engineering and economics will rely heavily on precision. With the rise of automation technologies, precise calculations will be executed with greater efficiency and accuracy, allowing industries to optimize their operations. Technologies like robotic process automation (RPA) and machine learning algorithms will automate tasks that currently require manual calculation, ensuring that every operation—whether it’s a simple subtraction like 90-7.814 or a complex formula—is completed accurately.

How Industries Will Continue to Rely on Accurate Mathematical Operations

As industries continue to advance, the reliance on accurate mathematical operations will only increase. Whether it’s for financial forecasting, scientific research, or engineering design, the need for precision in mathematical calculations, including simple expressions like 90-7.814, will continue to be a cornerstone of technological progress. As data becomes more abundant and models become more sophisticated, the demand for accuracy and precision will drive innovation and ensure that industries remain efficient and competitive.

Conclusion

Though seemingly simple, “90-7.814” represents much more than a basic subtraction operation. It symbolizes the importance of precision in all areas of life, from engineering and science to economics and data science. The ability to perform such calculations accurately is vital in ensuring that systems and models work as intended.

Small calculations like 90-7.814 are the foundation for larger, more complex models. Precision in these small adjustments leads to more reliable results in financial forecasting, engineering design, and scientific experiments, ensuring that the final outcomes are as accurate as possible.

Understanding the significance of 90-7.814 helps highlight the broader implications of mathematical precision in the world around us. From the design of infrastructure to the forecasting of economic trends,

precision in small calculations is fundamental to improving efficiency, ensuring reliability, and enhancing innovation across multiple industries. By valuing even the simplest operations, such as 90-7.814, we lay the groundwork for more accurate and reliable results in engineering designs, scientific experiments, and economic models.

When applied in real-world scenarios, these small adjustments amplify the precision of larger systems. For example, in engineering, a slight change in measurements could influence structural integrity, while in economics, minor cost adjustments can affect long-term profitability. Thus, it’s clear that mastering the art of precise calculation—no matter how seemingly insignificant—has widespread ramifications that affect everything from public safety to business profitability.

Frequently Asked Questions

Stay in touch to get more updates & alerts on Creative Released! Thank you